ΜΑΘΗΜΑΤΙΚΑ 16.11 - Παραγοντοποίηση φυσικών αριθμών

 

Παραγοντοποίηση φυσικών αριθμών

• Τι είναι;
 
• 
  
 
• 
  
 
• 
  
 
• 
  

Κάθε σύνθετος αριθμός μπορεί να γραφτεί σε παραγοντοποιημένη μορφή, δηλαδή σαν γινόμενο πρώτων παραγόντων.

• Ο αριθμός 60 γράφεται: 2 Χ 2 Χ 3 Χ 5

• Ποιοι αριθμοί;
 
• 
  

Μόνο οι σύνθετοι αριθμοί παραγοντοποιούνται. Ένας πρώτος αριθμός δεν μπορεί να γραφτεί σε παραγοντοποιημένη μορφή, γιατί γράφεται μόνο ως γινόμενο του ​1 επί τον εαυτό του.

• Ο αριθμός 91 (πρώτος αριθμός) μπορεί να γραφτεί ως 1 Χ 91

• Πώς γίνεται;
 
• 
  

Μπορούμε να αναλύσουμε ένα σύνθετο αριθμό σε γινόμενο πρώτων παραγόντων...

• με δεντροδιαγράμματα ή
• με διαδοχικές διαιρέσεις

• 1ος
 
• 
  

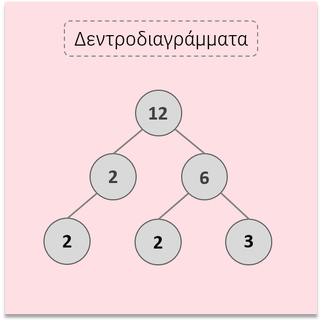
Δεντροδιαγράμματα

Γράφουμε το γινόμενο που μας δίνει τον αριθμό 12. Εδώ γράψαμε 2 Χ 6. Ο αριθμός 2 είναι πρώτος, οπότε συνεχίζουμε τη διαδικασία για τον αριθμό 6, του οποίου το γινόμενο είναι 2 Χ 3. Στην τρίτη σειρά γράφουμε τον αριθμό 2 και το γινόμενο 2 Χ 3. Η ανάλυση τελειώνει, όταν όλοι οι παράγοντες είναι πρώτοι αριθμοί όπως εδώ (2, 2 και 3). Άρα ο αριθμός 12 μπορεί να εκφραστεί ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3 2ος Διαδοχικές διαιρέσεις 1. Εξετάζουμε ποιος είναι ο μικρότερος πρώτος αριθμός που διαιρεί ακριβώς το 12. Είναι το 2. Διαιρούμε με το 2 και γράφουμε κάτω από το 6 το πηλίκο της διαίρεσης. 2. Συνεχίζουμε την ίδια διαδικασία για το 6. Διαιρούμε με το 2 και γράφουμε το πηλίκο της διαίρεσης που είναι το 3. 3. Το 3 δε διαιρείται με το 2. Πάμε στον επόμενο πρώτο αριθμό που είναι το 3 και εξετάζουμε αν διαιρείται με το 3. Διαιρούμε με το 3 και γράφουμε το πηλίκο της διαίρεσης που είναι το 1. 4. Αν το πηλίκο είναι η μονάδα τότε τελειώνει και η ανάλυση. Άρα ο αριθμός 12 εκφράζεται ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3